初识DDPM 算法理解（例会版）

DDPM 概率扩散模型

1. 前提引入：

1.1正态分布

正态分布是非常常见的连续几率随机分布。

对于一个骰子 假如我们随机掷骰子，随着次数的增多 每个点数出现的概率：

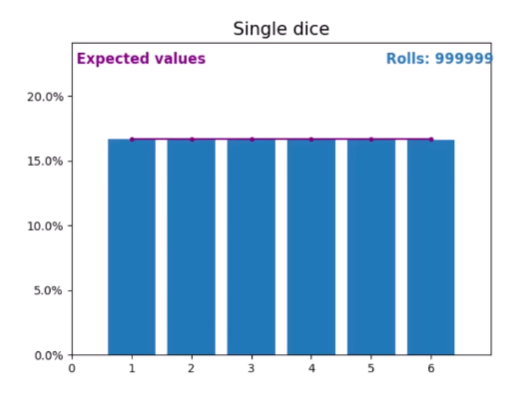
继续增加骰子，重复这个实验：

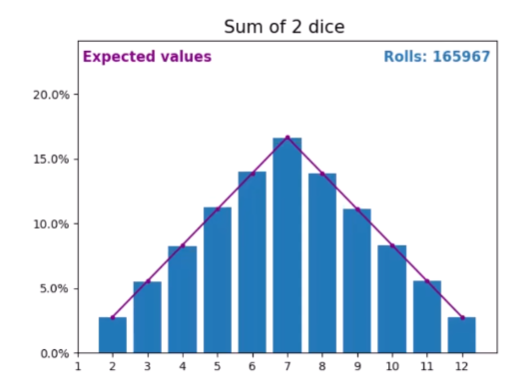
发现随着采样次数的增加 七点的值会逐渐增加成为一个折线

假设我们继续增加骰子，重复这个实验：

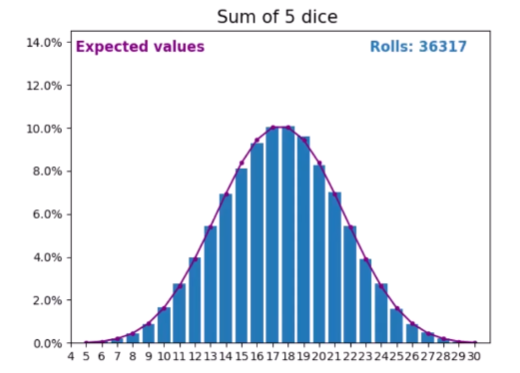
随着骰子数量的增多，折线越来越接近这样一个曲线 即为概率密度曲线

这样的概率分布在自然界中十分常见 即为Normal Distribution 正态分布

若随机变数服从一个平均数为、标准差为的常态分布，则记为：

则其概率密度函数为

μ为平均值，σ为标准差

1.2 扩散

扩散现象是自然界中很常见的一种现象 扩散现象（diffusion）是指物质分子从高浓度区域向低浓度区域转移直到均匀分布的现象

对于一张图片 我们是否可以有 通过对图片不断增加高斯噪声来模拟这个现象，并通过你想过程从随机噪声中生成图片？

2. DDPM:

2.1 前向过程：

前向过程即为对图片添加噪声的过程 那么我们怎么对一个图片添加高斯噪声呢？

相信学过深度学习的同学都知道 ，在处理图片数据集时 我们常采用处理图片数据的手段 对RGB通道 [x,y,z]进行归一化处理 然后做为维度特征 加入对一张图片来讲：

​ (●’◡’●)

取其中的一个像素点：

我们先将像素点的数值通过归一化 压缩到[-1.0,+1.0]区间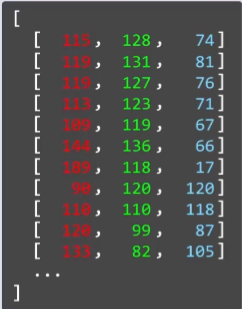

接下来我们来产生一个同样大小的噪声图片 对于每个像素点来说 我们通过高斯分布采样 对每个位置的值随机取样 所有像素通道数值遵从正态随机分布

接下来我们对噪声图片 和同尺寸需要加噪的进行混合 我们讲同一像素通道内数值 通过

$$\sqrt[]β×ε＋\sqrt[][1-β]×X$$

β∈[0,1] 观察该公式的两个系数可知，系数平方和刚好等于一，满足勾股定理 那么对于随着β的增加 x的占比会不断减小，两者之间是此消彼长的关系

这里演示图
那么我们现在得到了 如何对一个图片添加高斯噪音的方法了

对于这张图片 x0 x1 x2 x3 x4 x5 x6 x7

$$X_1 = \sqrt[]\beta_1 \times \epsilon_1 +\sqrt{1-\beta_1}\times x_0 \\ X_2 = \sqrt[]\beta_2 \times \epsilon_2 +\sqrt{1-\beta_2}\times x_1 \\ X_3 = \sqrt[]\beta_3 \times \epsilon_3 +\sqrt{1-\beta_3}\times x_2 \\$$

以此类推 使用此公式不断迭代直到$x_t$ , 我们可以用一个式子 来表达前一时刻和后一时刻的关系

$$X_t = \sqrt[]\beta_t \times \epsilon_t+\sqrt{1-\beta_t}\times x_{t-1} \\$$

每一步中加噪用到的 $\epsilon \backsim N(0,1)$ 基于标准正态分布重新采样的随机数 每一步中的$\beta$并不相同 ，随着时间的增加 β是逐渐趋于1的 因为扩散速度越来越快

为了便于 推导 我们假设$\alpha_t = 1-\beta_t$ 那么公式就转换为了 ：

$$X_t = \sqrt{1-\alpha_t} \times \epsilon_t+\sqrt{\alpha_t}\times x_{t-1}$$

问题：能不能直接从x0推导出xt 之间的关系呢？

现在得到了Xt和Xt-2的关系 对于参数$\epsilon$ 他是从正态随机分布采样出来的值 那么如前提所知 两个骰子的概率分布叠加后满足正态分布 ，

那么我们可不可以知道多种采样的的概率叠加呢

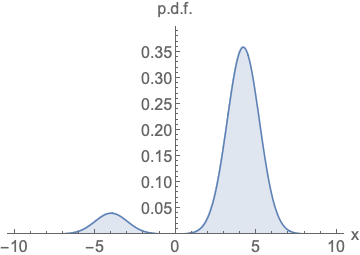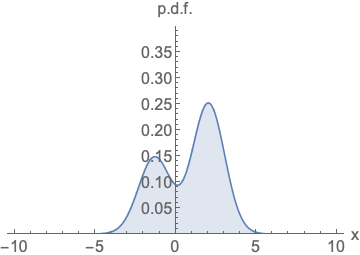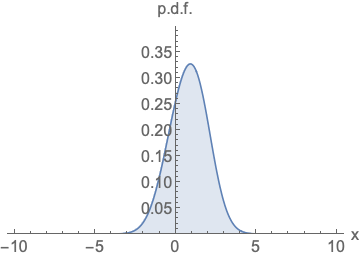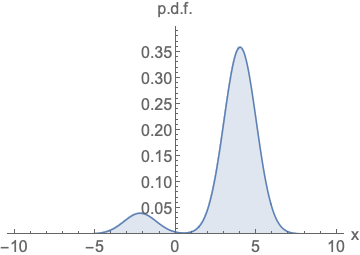
现对于两个正态分布的卷积依然是正态分布

那么对于上述式子 我们可以把 两次随机分布采样变为一次随机分布采样

分析上面的式子

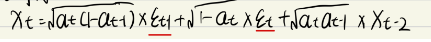
对于正态分布N(0,1) 如果乘一个常数m 那么平均值变为mμ，标准差变为mσ

根据定义我们可以很快的知道 对于一个叠加的正态分布 我们有

$$N(\mu_1,\sigma_1^2) + N(\mu_2,\sigma_2^2)=N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)$$

我们可以得出$N(0,\alpha_t-\alpha_t\alpha_{t-1}),N(0,1-\alpha_t)$是属于刚刚上面两个采样的分布的

那么他俩的叠加后的分布 根据公式可得 $N(0,\alpha_t-\alpha_t\alpha_{t-1}) +N(0,1-\alpha_t) = N(0,1-\alpha_t\alpha_{t-1})$

那么我们的Xt的公式可以改写为：

$$X_t = \sqrt{1-\alpha_t\alpha_{t-1}}\epsilon+\sqrt{\alpha_t\alpha_{t-1}}X_{t-1}$$

这种技巧叫做重参数化技巧

那么我可以递推出xt和xt-2之间的关系 ……..

通过数学归纳法 我们可以得出

这样我们就得到了Xt和X0的关系了

为了简化 方便描述 我们设$\bar \alpha = \alpha_t\alpha_{t-1}....\alpha_1$

很好 我们现在得出:

$$X_t = \sqrt{1-\bar\alpha}\epsilon+ \sqrt {\bar\alpha}X_0,\epsilon \backsim N(0,1)$$ $$q(x_{t}|x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-\bar{a}*{t}}} e^{\left ( -\frac{1}{2}\frac{(x*{t}-\sqrt{\bar{a}*{t}}x_0)^2}{1-\bar{a}*{t}} \right ) }$$

2.2 反向推理

通过刚刚的推导 我们理解了 在前向加噪的过程中发生的变化

那么我们的目的是反向去噪生成模型 这个怎么实现呢？

我们可以用此关系 反向推理求出和X0的关系

知识点 ：贝叶斯定理

我们的目标是$X_t = \sqrt{1-\bar\alpha}\epsilon_t+ \sqrt {\bar\alpha}X_{t-1}$

那么对于后验概率$p(X_{t-1}|X_t)=\cfrac{p(X_t|X_{t-1})p(X_{t-1})}{p(X_t)}$

分别为$X_t,X_{t-1}$时刻的概率 也就是从X0推断出的概率

所以 我们 可以用另外一个形式来表示

$$p(X_{t-1}|X_t,X_0)=\cfrac{p(X_t|X_{t-1},X_0)p(X_{t-1}|X_0)}{p(X_t|X_0)}$$

至此 只要求解右边的式子 我们就可以知道给定Xt时刻,前一时刻$X_{t-1}$的概率

$$x_{t} = \sqrt{a_t}x_{t-1}+\sqrt{1-a_t}\times ϵ$$ ~ $N(\sqrt{a_t}x_{t-1}, 1-a_{t})$ $$x_{t-1} = \sqrt{\bar{a}_{t-1}}x_0+ \sqrt{1-\bar{a}_{t-1}}\times ϵ$$ ~ $N( \sqrt{\bar{a}_{t-1}}x_0, 1-\bar{a}_{t-1})$ $$x_{t} = \sqrt{\bar{a}_{t}}x_0+ \sqrt{1-\bar{a}_{t}}\times ϵ$$ ~ $N( \sqrt{\bar{a}_{t}}x_0, 1-\bar{a}_{t})$ **既然我们已知了不同阶段的正态分布函数，通过概率密度函数 我们可以求出该时刻的概率 将三者概率带入到我们的朴素贝叶斯公式中可以得出** $$ q(x_{t}|x_{t-1},x_{0}) = \frac{1}{\sqrt{2\pi } \sqrt{1-a_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_{t}} \right ) }$$

推导过程如下：

$$\frac{ q(x_{t}|x_{t-1},x_{0})\times q(x_{t-1}|x_0)}{q(x_{t}|x_0)} = \left [ \frac{1}{\sqrt{2\pi} \sqrt{1-a_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_{t}} \right ) } \right ] * \left [ \frac{1}{\sqrt{2\pi} \sqrt{1-\bar{a}_{t-1}}} e^{\left ( -\frac{1}{2}\frac{(x_{t-1}-\sqrt{\bar{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} \right ) } \right ] \div \left [ \frac{1}{\sqrt{2\pi} \sqrt{1-\bar{a}_{t}}} e^{\left ( -\frac{1}{2}\frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) } \right ]$$ $$\Downarrow$$ $$\frac{\sqrt{2\pi} \sqrt{1-\bar{a}_{t}}}{\sqrt{2\pi} \sqrt{1-a_{t}} \sqrt{2\pi} \sqrt{1-\bar{a}_{t-1}} } e^{\left [ -\frac{1}{2} \left ( \frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_{t}} + \frac{(x_{t-1}-\sqrt{\bar{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) \right ] }$$ $$\Downarrow$$ $$\frac{1}{\sqrt{2\pi} \left ( \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}} } {\sqrt{1-\bar{a}_{t}}} \right ) } exp{\left [ -\frac{1}{2} \left ( \frac{(x_{t}-\sqrt{a_t}x_{t-1})^2}{1-a_t} + \frac{(x_{t-1}-\sqrt{\bar{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right ) \right ] }$$ $$\Downarrow$$ $$\frac{1}{\sqrt{2\pi} \left ( \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}} } {\sqrt{1-\bar{a}_{t}}} \right ) } exp \left[ -\frac{1}{2} \left ( \frac{ x_{t}^2-2\sqrt{a_t}x_{t}x_{t-1}+{a_t}x_{t-1}^2 }{1-a_t} + \frac{ x_{t-1}^2-2\sqrt{\bar{a}_{t-1}}x_0x_{t-1}+\bar{a}_{t-1}x_0^2 }{1-\bar{a}_{t-1}} - \frac{(x_{t}-\sqrt{\bar{a}_{t}}x_0)^2}{1-\bar{a}_{t}} \right) \right]$$ $$\Downarrow$$ $$\frac{1}{\sqrt{2\pi} \left ( {\color{Red} \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}} } {\sqrt{1-\bar{a}_{t}}}} \right ) } exp \left[ -\frac{1}{2} \frac{ \left( x_{t-1} - \left( {\color{Purple} \frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t}x_t + \frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t}x_0} \right) \right) ^2 } { \left( {\color{Red} \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}} } {\sqrt{1-\bar{a}_{t}}}} \right)^2 } \right]$$ $$\Downarrow$$ $$p(x_{t-1}|x_{t}) \sim N\left( {\color{Purple} \frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t}x_t + \frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t}x_0} , \left( {\color{Red} \frac{ \sqrt{1-a_t} \sqrt{1-\bar{a}_{t-1}} } {\sqrt{1-\bar{a}_{t}}}} \right)^2 \right)$$

求得反向推导的函数公式为

又因为 $x_{t} = \sqrt{\bar{a}_t}\times x_0+ \sqrt{1-\bar{a}_t}\times ϵ$, $x_0 = \frac{x_t - \sqrt{1-\bar{a}_t}\times ϵ}{\sqrt{\bar{a}_t}}$. 代换如上述函数可得

$$p(x_{t-1}|x_{t}) \sim N\left( {\color{Purple} \frac{\sqrt{a_t}(1-\bar{a}_{t-1})}{1-\bar{a}_t}x_t + \frac{\sqrt{\bar{a}_{t-1}}(1-a_t)}{1-\bar{a}_t}\times \frac{x_t - \sqrt{1-\bar{a}_t}\times ϵ}{\sqrt{\bar{a}_t}} } , {\color{Red} \frac{ \beta_{t} (1-\bar{a}_{t-1}) } { 1-\bar{a}_{t}}} \right)$$

由此 我们知道 怎么通过概率反向推出原图片的过程

3.3 代码实现

通过上述的问题 我们可以了解到 DDPM模型 在神经网络中的结构

详细见colab DF